 12-23-2008, 08:27 AM
12-23-2008, 08:27 AM
|
#8 (permalink)
|
|
Addict
|
Quote:
Originally Posted by Rekna
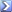
Are you assuming the starbursts colors and orientation have a completely equal distribution? Without that assumption your first 2 questions are impossible to answer.
This one is pretty easy is you generalize it for order.
Spoiler:
First you need to calculate the odds of rolling this in order.
To do this you multiply the odds of rolling 2-12 individually and then multiply by the number of orders you can roll it.
odds for 7 xxxxxxxx
odds for 6 and 8 xxxxxxx
odds for 5 and 9 xxxxxxx
odds for 4 and 10 xxxxxxx
odds for 3 and 11 xxxxxxx
odds for 2 and 12 xxxxxxx
Multiply them together and you get:
(xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx)
this is the probability of rolling in a specific order. Now you have one of these for each possible way to order the rolls.
To compute the number of orders you will need to use a partial factorial.
The first roll has xx possibilities (xxxxxx). After each roll the number of possibilities drops by one. Thus you have a partial factorial. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
Multiplying the odds for one order above yields a probability of: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
It has been a few years since I have done any probability & stats how did I do?
|
Just from basic logic of probability (Forgive me some for it has been several years since I took Probability and Statistics in school) But....
Spoiler:
Basic numbers show that the odds of doing the die roll in sequence is MUCH higher than approx 1 in 36,000. just to have the chance of rolling a 2 then a 3 immediately after is 1:2916, then the odds of a 4 following THAT is 1:145800...etc... I dont have the time to go on much further, but as you can tell, it is exponentionally growing, so I am going to estimate that the odds of rolling 2,3,4,5,6,7,8,9,10,11,12 would be in the neighborhood of 1: "billions"
"Statistics of Dice Throw
The probababilities of different numbers obtained by the throw of two dice offer a good introduction to the ideas of probability. For the throw of a single die, all outcomes are equally probable. But in the throw of two dice, the different possibilities for the total of the two dice are not equally probable because there are more ways to get some numbers than others. There are six ways to get a total of 7, but only one way to get 2, so the "odds" of getting a 7 are six times those for getting "snake eyes". This simple example raises the idea of distinguishable states. For example, throwing a 3 is twice as likely as throwing a 2 because there are two distinguishable ways to get a 3. "
Taken from
Statistics of Dice Throw
__________________
"It is not that I have failed, but that I have found 10,000 ways that it DOESN'T work!" --Thomas Edison
|

|
|