Quote:
Originally Posted by Jozrael
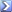
How do I prove that 2^n + 3^n - 5^n is always divisible by 6?
|
Ok here you go:
assume that 2^n + 3 ^n - 5^n is divisible by 6
base case: 2^2+3^2-5^2=-12
inductive step:
2^(n+1)+3^(n+1)-5^(n+1)
=2*2^n+ 3*3^n -5*5^n
=2^n+2^n+3^n+3^n+3^n-5^n-5^n-5^n-5^n-5^n
= (2^n+3^n+5^n)+(2^n+3^n+5^n) + (3^n -3*5^n)
The first 2 terms are both divisible by 6 (from our assumption) but is the 3rd?
We can try induction on that one to prove it
assume 3^n -3*5^n is divisible by 6
base case: 3^2 - 3*5^2 = -66
inductive step
3^(n+1) - 3*5^(n+1)
=3*3^n - 3*5*5^n
=3^n+3^n+3^n-3*(5^n+5^n+5^n+5^n+5^n)
=(3^n-3*5^n)+(3^n-3*5^n)+(3^n-3*5^n)-3*2(5^n)
=(3^n-3*5^n)+(3^n-3*5^n)+(3^n-3*5^n)-6(5^n)
The first 3 terms are divisible by 6 from the assumption and the 4th term is divisible by 6 because it is multiplied by 6. Thus 3^n -3*5^n is divisible by 6 and as a result 2^n + 3 ^n - 5^n is divisible by 6.
QED.
Please check my work.